Bavo Robben* and Lieven Penninck*
*PlanOpSim NV, Gent 9000, Belgium.
bavo.robben@planopsim.com
Reading time: 9 minutes
Written for: optical engineers, photonics engineers, researchers, technology scouts
Extra-relevant if you are interested in: meta-surfaces, simulation accuracy, quality improvement
Local periodic approximation analysis is fast and easy scalable, but sometimes inaccurate. Full wave calculations are very slow and scale badly. In this article we discuss a happy middle calculation method called ‘overlapping domain analysis’ with increased accuracy and feasible calculation resources.
Limitations of ‘basic’ simulations: heavy full wave vs inaccurate LPA
Meta-surface design is often a balance between fast calculations and accuracy. The most distinct ways would be at one hand full wave based optimization (e.g. adjoint optimization) resulting in a rigorous solution at the expense of very long simulation times and small active areas of a few 10 µm2 while on the other hand is a library based approach where full wave simulation of individual meta-atoms is combined with local periodic approximation (LPA) based calculations to combine them into a large area meta-surface.
For analysis after optimization, the same calculation method is needed. In an analysis the calculation is performed only once since no iterations are needed. For this reason there is more margin to improve the accuracy in a large area meta-surface analysis than compared to LPA, while still keeping reasonable calculation times.
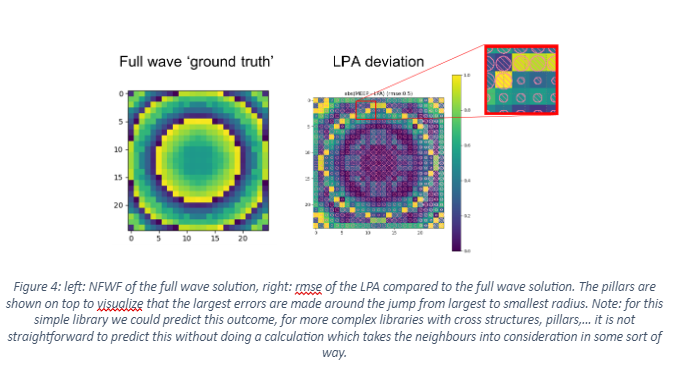
The approximation made by LPA is that the meta-atom is treated as if it was part of a repeating grid of identical structures. Each RCWA calculation assumes a periodic boundary condition as shown in Figure 1. As long as the neighbouring meta-atoms are the same or very similar, this approximation is valid. If the neighbouring meta-atoms are strongly different from one another this approximation no longer applies. This results in deviations in the calculation.
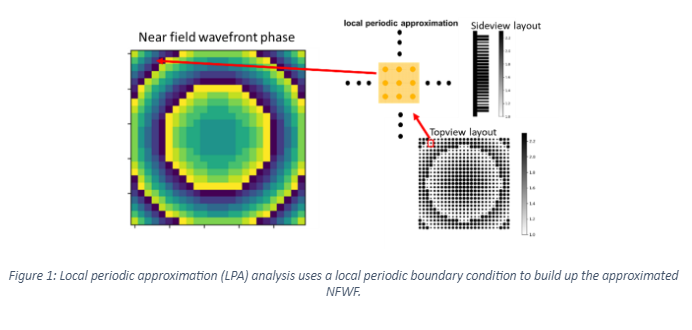
A simple example of this situation is a meta-lens with circular pillars as meta-atoms. A library of pillars is built to cover a 2π phase coverage as shown in Figure 2. In this simple library, we can already predict that the LPA calculation will be inaccurate around the phase delay value of -10° within a meta-surface, since the structures will suddenly have to change between the largest and the smallest one. Note: a common misconception is that there would be an issue for the phase jump from -180° to +180°. In fact this phase jump is completely arbitrary because a constant offset in phase has no functional effect on the phase. In other words only differences in phase are important not the absolute level. The change in radius of the actual structure in the -180° is smoothly increasing from 130nm to 140nm, so neighbouring effects will be small.
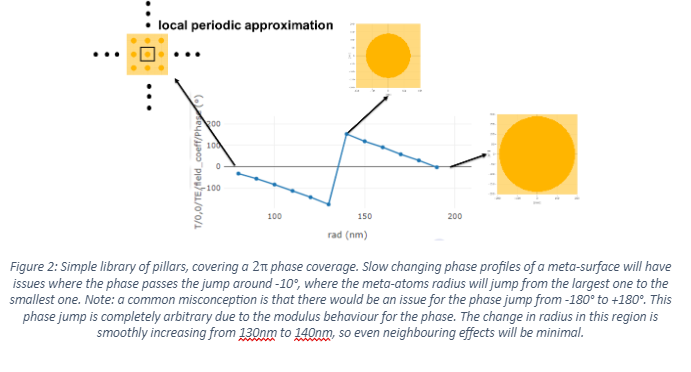
Carefully looking at Figure 1 shows indeed that LPA doesn’t take this neighbouring effect into account, the phase changes smoothly over the whole area, the sudden 2π jump is as noted above on a rather arbitrary location and is not a source of increased aberrations.
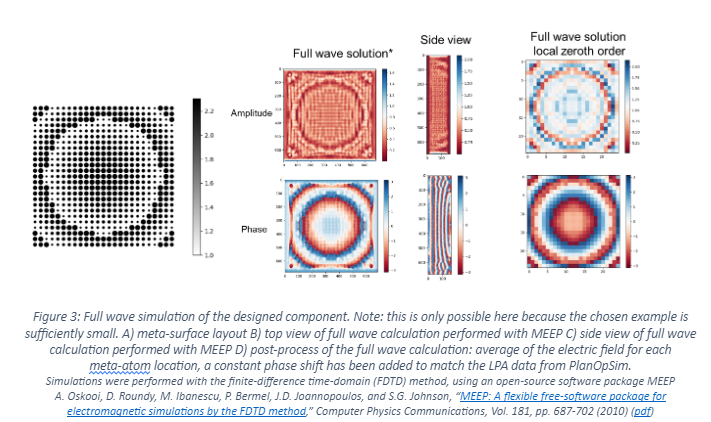
If we look at the full wave analysis of this component (in general this is impossible, we can only do this here because this meta-surface is sufficiently small!) in Figure 3 we can see that the sudden change in radius is indeed affecting the near field wavefront.
This non-local effect is even more clearly visible when plotting the root mean square error of the LPA phase compared to the full wave solution, as visualized in Figure 4.
Practical solutions to include neighbour to neighbour effects: ODA
As mentioned, this full wave ‘ground truth’ calculation is not feasible in general situations due to memory limitations and extreme simulation times. With Overlapping domain analysis (ODA) we have an intermediate analysis type which takes a fixed number of neighbours into account, resulting in improved analysis within a feasible memory and time frame.
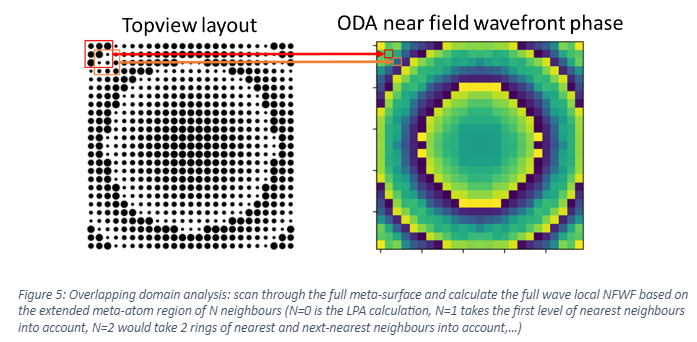
Within PlanOpSim we can select the incident and exit light properties and calculate the ODA-NFWF. In the background it will automatically scan through the whole meta-surface, create supercells of 3 by 3 neighbours and calculate the local near field on the central meta-atom. Since this is roughly an N by N RCWA calculation of accuracy 3x (acc_x_single_meta-atom, acc_y_single_meta-atom), this becomes a feasible but long calculation. Since all calculations are independent, a strong benefit compared to full wave calculation is the possibility of parallelization, depending on the workstation. It is still advised to limit the meta-atom accuracy to (4,4).
In Figure 6 the deviation from the full wave solution is compared between the LPA analysis and ODA. A general improvement is noticeable, and especially in the region where the LPA fails to capture the radius jump, the ODA has a strongly reduced error.
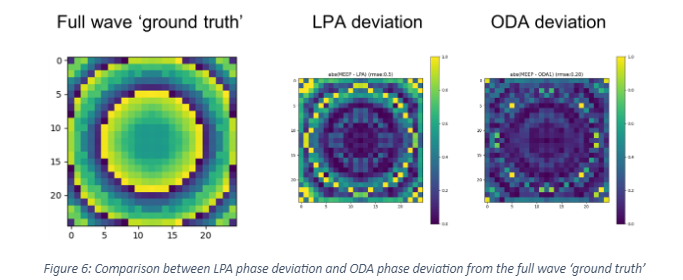
What does this result mean in practice? First of all we have a more accurate result available. Bringing this NFWF to FFWF analysis, fourier analysis or a ray tracing link will provide a more accurate result. Where the design itself did not include neighbouring effects of the meta-atoms, we are now able to actually correctly capture wavefront errors due to these. An expected result is that we now can more accurately visualize the reduced focussing efficiency for meta-lenses or a zeroth order error spot for holographic meta-surfaces.
Conclusion
With ODA a new analysis tool is added within the PlanOpSim software metacomponent module to be able to more accurately verify the created design by taking into account the neighbour to neighbour interactions of meta-atoms. The improved ODA-NFWF can be used for an improved NFWF analysis, FFWF analysis, Fourier analysis and ray tracing link.
Further reading
Zin Lin and Steven G. Johnson, “Overlapping domains for topology optimization of large-area metasurfaces,” Opt. Express 27, 32445-32453 (2019)